Class float3x3
Summary
A 3-by-3 matrix for linear transformations of 3D geometry.
Description
This matrix can represent any kind of linear transformations of 3D geometry, which include rotation, scale, shear, mirroring and orthographic projection. A 3x3 matrix cannot represent translation (which requires a 3x4 matrix), or perspective projection (which requires a 4x4 matrix).
The elements of this matrix are
The element m_yx is the value on the row y and column x. You can access m_yx using the double-bracket notation m[y][x], or using the member function m.At(y, x);
The member functions in this class use the convention that transforms are applied to vectors in the form M * v. This means that "float3x3 M, M1, M2; M = M1 * M2;" gives a transformation M that applies M2 first, followed by M1 second, i.e. M * v = M1 * M2 * v = M1 * (M2 * v). This is the convention commonly used with OpenGL. The opposing convention (v * M) is commonly used with Direct3D. This class uses row-major storage, which means that the elements are packed in memory in order m[0][0], m[0][1], m[0][2], m[0][3], m[1][0], m[1][1], ... The elements for a single row of the matrix hold successive memory addresses. This is the same memory layout as with C++ multidimensional arrays.
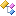float3x3
