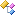 float3x3[Class Summary] float3x3[Class Summary] |
 v v |
 zero[static][const] zero[static][const] |
 identity[static][const] identity[static][const] |
 nan[static][const] nan[static][const] |
 ctor (+3 overloads) ctor (+3 overloads) |
 ToQuat()[const] ToQuat()[const] |
 GetScale()[const] GetScale()[const] |
 operator[](row) (+1 overload) operator[](row) (+1 overload) |
 At(row,col) (+1 overload) At(row,col) (+1 overload) |
 Row(row) (+1 overload) Row(row) (+1 overload) |
 Row3(row) (+1 overload) Row3(row) (+1 overload) |
 Col(col)[const] Col(col)[const] |
 Col3(col)[const] Col3(col)[const] |
 Diagonal()[const] Diagonal()[const] |
 ScaleRow(row,scalar) ScaleRow(row,scalar) |
 ScaleCol(col,scalar) ScaleCol(col,scalar) |
 PositiveX/Y/Z()[const] PositiveX/Y/Z()[const] |
 ptr() (+1 overload) ptr() (+1 overload) |
 SetRow(row,data) (+2 overloads) SetRow(row,data) (+2 overloads) |
 SetCol(column,data) (+2 overloads) SetCol(column,data) (+2 overloads) |
 Set(...) (+3 overloads) Set(...) (+3 overloads) |
 SetIdentity() SetIdentity() |
 SwapColumns(col1,col2) SwapColumns(col1,col2) |
 SwapRows(row1,row2) SwapRows(row1,row2) |
 SetRotatePart/X/Y/Z(...) (+1 overload) SetRotatePart/X/Y/Z(...) (+1 overload) |
 operator=(rhs) (+1 overload) operator=(rhs) (+1 overload) |
 Determinant()[const] Determinant()[const] |
 DeterminantSymmetric()[const] DeterminantSymmetric()[const] |
 Inverse(epsilon) Inverse(epsilon) |
 InverseFast(epsilon) InverseFast(epsilon) |
 SolveAxb(b,x)[const] SolveAxb(b,x)[const] |
 Inverted()[const] Inverted()[const] |
 InverseColOrthogonal() InverseColOrthogonal() |
 InverseOrthogonalUniformScale() InverseOrthogonalUniformScale() |
 InverseOrthonormal() InverseOrthonormal() |
 InverseSymmetric() InverseSymmetric() |
 Transpose() Transpose() |
 Transposed()[const] Transposed()[const] |
 InverseTranspose() InverseTranspose() |
 InverseTransposed()[const] InverseTransposed()[const] |
 Trace()[const] Trace()[const] |
 Orthonormalize(...) Orthonormalize(...) |
 RemoveScale() RemoveScale() |
 Transform(vector)[const] (+1 overload) Transform(vector)[const] (+1 overload) |
 TransformLeft(lhs)[const] TransformLeft(lhs)[const] |
 Transform(vector)[const] Transform(vector)[const] |
 BatchTransform(...)[const] (+3 overloads) BatchTransform(...)[const] (+3 overloads) |
 operator*(rhs)[const] (+4 overloads) operator*(rhs)[const] (+4 overloads) |
 operator/(scalar)[const] operator/(scalar)[const] |
 operator+(rhs)[const] operator+(rhs)[const] |
 operator-(rhs)[const] (+1 overload) operator-(rhs)[const] (+1 overload) |
 operator+()[const] operator+()[const] |
 operator*=(scalar) operator*=(scalar) |
 operator/=(scalar) operator/=(scalar) |
 operator+=(rhs) operator+=(rhs) |
 operator-=(rhs) operator-=(rhs) |
 IsFinite()[const] IsFinite()[const] |
 IsIdentity(epsilon)[const] IsIdentity(epsilon)[const] |
 IsLowerTriangular(epsilon)[const] IsLowerTriangular(epsilon)[const] |
 IsUpperTriangular(epsilon)[const] IsUpperTriangular(epsilon)[const] |
 IsInvertible(epsilon)[const] IsInvertible(epsilon)[const] |
 IsSymmetric(epsilon)[const] IsSymmetric(epsilon)[const] |
 IsSkewSymmetric(epsilon)[const] IsSkewSymmetric(epsilon)[const] |
 HasUnitaryScale(epsilonSq)[const] HasUnitaryScale(epsilonSq)[const] |
 HasNegativeScale()[const] HasNegativeScale()[const] |
 HasUniformScale(epsilon)[const] HasUniformScale(epsilon)[const] |
 IsRowOrthogonal(epsilon)[const] IsRowOrthogonal(epsilon)[const] |
 IsColOrthogonal(epsilon)[const] IsColOrthogonal(epsilon)[const] |
 IsColOrthogonal3(epsilon)[const] IsColOrthogonal3(epsilon)[const] |
 IsOrthonormal(epsilon)[const] IsOrthonormal(epsilon)[const] |
 Equals(other,epsilon)[const] Equals(other,epsilon)[const] |
 ToString()[const] ToString()[const] |
 SerializeToString()[const] SerializeToString()[const] |
 ToString2()[const] ToString2()[const] |
 ToEuler***()[const] ToEuler***()[const] |
 ExtractScale()[const] ExtractScale()[const] |
 Decompose(rotate,scale)[const] (+1 overload) Decompose(rotate,scale)[const] (+1 overload) |
 Mul(rhs)[const] (+5 overloads) Mul(rhs)[const] (+5 overloads) |
 MulPos(rhs)[const] (+1 overload) MulPos(rhs)[const] (+1 overload) |
 MulDir(rhs)[const] (+1 overload) MulDir(rhs)[const] (+1 overload) |
 RotateX/Y/Z(angleRadians)[static] RotateX/Y/Z(angleRadians)[static] |
 RotateAxisAngle(...)[static] RotateAxisAngle(...)[static] |
 RotateFromTo(...)[static] RotateFromTo(...)[static] |
 LookAt(...)[static] LookAt(...)[static] |
 RandomRotation(lcg)[static] RandomRotation(lcg)[static] |
 RandomGeneral(...)[static] RandomGeneral(...)[static] |
 FromQuat(orientation)[static] FromQuat(orientation)[static] |
 FromRS(rotate,scale)[static] (+1 overload) FromRS(rotate,scale)[static] (+1 overload) |
 FromEuler***(ex,ey,ex2)[static] FromEuler***(ex,ey,ex2)[static] |
 Scale(sx,sy,sz)[static] (+1 overload) Scale(sx,sy,sz)[static] (+1 overload) |
 ScaleAlongAxis(axis,scalingFactor)[static] ScaleAlongAxis(axis,scalingFactor)[static] |
 UniformScale(uniformScale)[static] UniformScale(uniformScale)[static] |
 ShearX/Y/Z(yFactor,zFactor)[static] ShearX/Y/Z(yFactor,zFactor)[static] |
 Mirror(p)[static] Mirror(p)[static] |
 OrthographicProjection/YZ/XZ/XY(target)[static] OrthographicProjection/YZ/XZ/XY(target)[static] |
float3x3::ToEuler***
Syntax
float3 float3x3::ToEulerXYX() const; [1 line of code]float3 float3x3::ToEulerXZX() const; [1 lines of code]
float3 float3x3::ToEulerYXY() const; [1 lines of code]
float3 float3x3::ToEulerYZY() const; [1 lines of code]
float3 float3x3::ToEulerZXZ() const; [1 lines of code]
float3 float3x3::ToEulerZYZ() const; [1 lines of code]
float3 float3x3::ToEulerXYZ() const; [1 lines of code]
float3 float3x3::ToEulerXZY() const; [1 lines of code]
float3 float3x3::ToEulerYXZ() const; [1 lines of code]
float3 float3x3::ToEulerYZX() const; [1 lines of code]
float3 float3x3::ToEulerZXY() const; [1 lines of code]
float3 float3x3::ToEulerZYX() const; [1 lines of code]
Extracts the rotation part of this matrix into Euler rotation angles (in radians).
Note
It is better to think about the returned float3 as an array of three floats, and not as a triple of xyz, because e.g. the .y component returned by ToEulerYXZ() does not return the amount of rotation about the y axis, but contains the amount of rotation in the second axis, in this case the x axis.