Class float4x4
Summary
A 4-by-4 matrix for affine transformations and perspective projections of 3D geometry.
Description
This matrix can represent the most generic form of transformations for 3D objects, including perspective projections, which float3x4 cannot store, and translations, which float3x3 cannot represent.
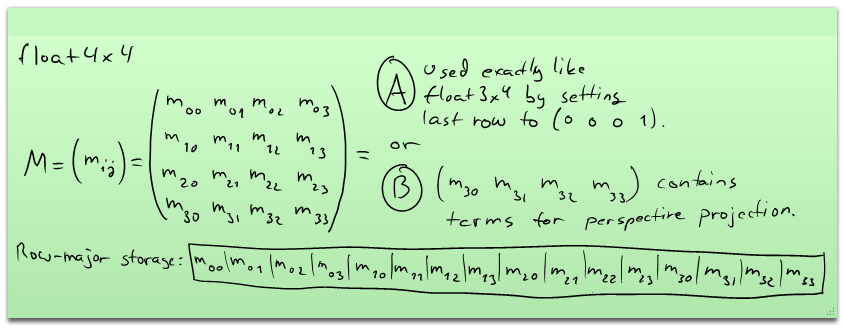
The elements of this matrix are
The element m_yx is the value on the row y and column x. You can access m_yx using the double-bracket notation m[y][x], or using the member function m.At(y, x);
The member functions in this class use the convention that transforms are applied to vectors in the form M * v. This means that "float4x4 M, M1, M2; M = M1 * M2;" gives a transformation M that applies M2 first, followed by M1 second, i.e. M * v = M1 * M2 * v = M1 * (M2 * v). This is the convention commonly used with OpenGL. The opposing convention (v * M) is commonly used with Direct3D. This class uses row-major storage, which means that the elements are packed in memory in order m[0][0], m[0][1], m[0][2], m[0][3], m[1][0], m[1][1], ... The elements for a single row of the matrix hold successive memory addresses. This is the same memory layout as with C++ multidimensional arrays.
 float4x4
float4x4

