Class float3
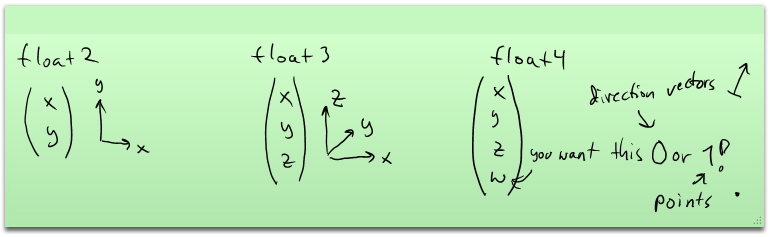
Summary
A vector of form (x,y,z).
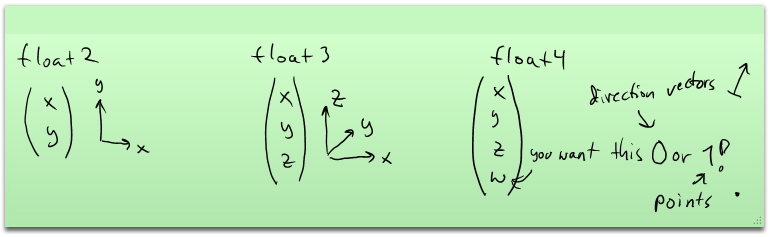
A vector of form (x,y,z).
 float3 | A vector of form (x,y,z). |
 x | The x component. |
| y | The y component. |
| z | The z component. |
| zero[static][const] | Specifies a compile-time constant float3 with value (0, 0, 0). |
| one[static][const] | Specifies a compile-time constant float3 with value (1, 1, 1). |
| unitX[static][const] | Specifies a compile-time constant float3 with value (1, 0, 0). |
| unitY[static][const] | Specifies a compile-time constant float3 with value (0, 1, 0). |
| unitZ[static][const] | Specifies a compile-time constant float3 with value (0, 0, 1). |
| nan[static][const] | A compile-time constant float3 with value (NaN, NaN, NaN). |
| inf[static][const] | A compile-time constant float3 with value (+infinity, +infinity, +infinity). |
 ctor (+4 overloads) | The default constructor does not initialize any members of this class. |
| ptr() (+1 overload) | Casts this float3 to a C array. |
 operator[](index) (+1 overload) | Accesses an element of this vector using array notation. |
| At(index) (+1 overload) | Accesses an element of this vector. |
| operators +,-,*,/(v)[const] (+1 overload) | Adds two vectors. |
| operators +=,-=,*=,/=(v) | Adds a vector to this vector, in-place. |
| Add/Sub/Mul/Div(v)[const] (+1 overload) | Adds a vector to this vector. |
| xx/xy/xz/..()[const] | Performs a 2D swizzled access to this vector. |
| xyz/xzy/yzx/..()[const] | Performs a 3D swizzled access to this vector. |
| Swizzled(i,j,k,l)[const] (+2 overloads) | Performs a swizzled access to this vector. |
| SetFromScalar(scalar) | Fills each entry of this float3 by the given scalar. |
| Set(x,y,z) | Sets all elements of this vector. |
| SetFromSphericalCoordinates(...) (+2 overloads) | Converts the given vector represented in spherical coordinates to an euclidean float3 (x,y,z) triplet. |
| ToPos4()[const] | Returns float4(x,y,z,1). |
| ToDir4()[const] | Returns float4(x,y,z,0). [similarOverload: ToPos4] |
| ToSphericalCoordinates()[const] | Converts this euclidean (x,y,z) float3 to spherical coordinates representation in the form (azimuth, inclination, radius). |
| ToSphericalCoordinatesNormalized()[const] | Converts this normalized euclidean (x,y,z) float3 to spherical coordinates representation in the form (azimuth, inclination) |
| Length()[const] | Computes the length of this vector. |
| LengthSq()[const] | Computes the squared length of this vector. |
| Normalize() | Normalizes this float3. |
| Normalized()[const] | Returns a normalized copy of this vector. |
| ScaleToLength(newLength) | Scales this vector so that its new length is as given. |
| ScaledToLength(newLength)[const] | Returns a scaled copy of this vector which has its new length as given. |
| IsNormalized(epsilonSq)[const] | Tests if the length of this vector is one, up to the given epsilon. |
| IsZero(epsilonSq)[const] | Tests if this is the null vector, up to the given epsilon. |
| IsFinite()[const] | Tests if this vector contains valid finite elements. |
| IsPerpendicular(other,epsilonSq)[const] | Tests if two vectors are perpendicular to each other. |
| Equals(other,epsilon)[const] (+1 overload) | Tests if two vectors are equal, up to the given epsilon. |
| BitEquals(other)[const] | Compares whether this float3 and the given float3 are identical bit-by-bit in the underlying representation. |
| ToString()[const] | Returns "(x, y, z)". |
| SerializeToString()[const] | Returns "x,y,z". This is the preferred format for the float3 if it has to be serialized to a string for machine transfer. |
| SerializeToCodeString()[const] | Returns a string of C++ code that can be used to construct this object. Useful for generating test cases from badly behaving objects. |
| SumOfElements()[const] | Returns x + y + z. |
| ProductOfElements()[const] | Returns x * y * z. |
| AverageOfElements()[const] | Returns (x+y+z)/3. |
| MinElement()[const] | Returns min(x, y, z). |
| MinElementIndex()[const] | Returns the index that has the smallest value in this vector. |
| MaxElement()[const] | Returns max(x, y, z). |
| MaxElementIndex()[const] | Returns the index that has the smallest value in this vector. |
| Abs()[const] | Takes the element-wise absolute value of this vector. |
| Neg()[const] | Returns a copy of this vector with each element negated. |
| Recip()[const] | Computes the element-wise reciprocal of this vector. |
| Min(ceil)[const] (+1 overload) | Returns an element-wise minimum of this and the vector (ceil, ceil, ceil). |
| Max(floor)[const] (+1 overload) | Returns an element-wise maximum of this and the vector (floor, floor, floor). |
| Clamp(floor,ceil)[const] (+1 overload) | Returns a vector that has floor <= this[i] <= ceil for each element. |
| Clamp01()[const] | Limits each element of this vector in the range [0, 1]. |
| ClampLength(maxLength)[const] (+1 overload) | Returns a copy of this vector, with its length scaled down to maxLength. |
| Distance(point)[const] (+9 overloads) | Computes the distance between this point and the given object. |
| DistanceSq(point)[const] | Computes the squared distance between this and the given point. |
| Dot(v)[const] | Computes the dot product of this and the given vector. |
| Cross(v)[const] | Computes the cross product of this and the given vector. |
| OuterProduct(rhs)[const] | Computes the outer product of this and the given vector. |
| Perpendicular(hint,hint2)[const] | Computes a new normalized direction vector that is perpendicular to this vector and the specified hint vector. |
| AnotherPerpendicular(hint,hint2)[const] | Returns another vector that is perpendicular to this vector and the vector returned by Perpendicular(). |
| PerpendicularBasis(outB,outC)[const] | This function computes two new vectors b and c which are both orthogonal to this vector and to each other. |
| RandomPerpendicular(rng)[const] | Generates a random vector that is perpendicular to this vector. |
| Reflect(normal)[const] | Returns this vector reflected about a plane with the given normal. |
| Refract(...)[const] | Refracts this vector about a plane with the given normal. |
| ProjectTo(direction)[const] | Projects this vector onto the given unnormalized direction vector. |
| ProjectToNorm(direction)[const] | Projects this vector onto the given normalized direction vector. |
| AngleBetween(other)[const] | Returns the angle between this vector and the specified vector, in radians. |
| AngleBetweenNorm(normalizedVector)[const] | Returns the angle between this vector and the specified normalized vector, in radians. |
| Decompose(...)[const] | Breaks this vector down into parallel and perpendicular components with respect to the given direction. |
| Lerp(b,t)[const] | Linearly interpolates between this and the vector b. |
| FromScalar(scalar)[static] | Generates a new float3 by filling its entries by the given scalar. |
| FromSphericalCoordinates(...)[static] (+2 overloads) | |
| AreCollinear(p1,p2,p3,epsilonSq)[static] | Tests if the points p1, p2 and p3 lie on a straight line, up to the given epsilon. |
| FromString(str,outEndStr)[static] (+1 overload) | Parses a string that is of form "x,y,z" or "(x,y,z)" or "(x;y;z)" or "x y z" to a new float3. |
| ScalarTripleProduct(u,v,w)[static] | Computes the scalar triple product of the given three vectors. |
| Lerp(a,b,t)[static] | This function is the same as calling a.Lerp(b, t). |
| Orthogonalize(a,b)[static] (+1 overload) | Makes the given vectors linearly independent. |
| AreOrthogonal(a,b,epsilon)[static] (+1 overload) | Returns true if the given vectors are orthogonal to each other. |
| Orthonormalize(a,b)[static] (+1 overload) | Makes the given vectors linearly independent and normalized in length. |
| AreOrthonormal(a,b,epsilon)[static] (+1 overload) | Returns true if the given vectors are orthogonal to each other and all of length 1. |
| RandomDir(lcg,length)[static] | Generates a direction vector of the given length. |
| RandomSphere(lcg,center,radius)[static] | Generates a random point inside a sphere. |
| RandomBox(...)[static] (+2 overloads) | Generates a random point inside an axis-aligned box. |
| RandomGeneral(...)[static] |