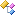 Sphere[Class Summary] |
 pos |
| r |
 ctor (+4 overloads) |
| Translate(offset) |
| Transform(transform) (+3 overloads) |
| MinimalEnclosingAABB()[const] |
| MaximalContainedAABB()[const] |
| SetNegativeInfinity() |
| Volume()[const] |
| SurfaceArea()[const] |
| Diameter()[const] |
| Centroid()[const] |
| AnyPointFast()[const] |
| ExtremePoint(direction)[const] (+1 overload) |
| ProjectToAxis(...)[const] |
| IsFinite()[const] |
| IsDegenerate()[const] |
| SetDegenerate() |
| Contains(point)[const] (+11 overloads) |
| Distance(point)[const] (+9 overloads) |
| MaxDistance(point)[const] |
| ClosestPoint(point)[const] |
| Intersects(...)[const] (+11 overloads) |
| Enclose(point,epsilon) (+10 overloads) |
| ExtendRadiusToContain(point,epsilon) (+1 overload) |
| RandomPointInside(lcg) |
| RandomPointOnSurface(lcg) |
| Triangulate(...)[const] |
| ToString()[const] |
| SerializeToString()[const] |
| SerializeToCodeString()[const] |
| Equals(rhs,epsilon)[const] |
| BitEquals(other)[const] |
| FastEnclosingSphere(...)[static] |
| OptimalEnclosingSphere(...)[static] (+4 overloads) |
| FitThroughPoints(a,b)[static] (+2 overloads) |
| RandomPointInside(lcg,center,radius)[static] |
| RandomPointOnSurface(lcg,center,radius)[static] |
| RandomUnitaryFloat3(lcg)[static] |
| IntersectLine(...)[static] |
| FromString(str,outEndStr)[static] (+1 overload) |
Sphere::IntersectLine
Syntax
int Sphere::IntersectLine(const float4 &linePos, const float4 &lineDir, const float4 &sphereCenter, float sphereRadius, float &t1, float &t2); [74 lines of code]Computes the intersection of a line and a sphere.
This function solves the points of intersection between a line and a sphere. A line intersects sphere at 0, 1 or 2 points. When only one point of intersection is reported, the given line is tangent to the sphere.
Note
The outputted variables t1 and t2 always satisfy t1 < t2. This allows distinguishing between the "enter" and "exit" positions of the line, if the line is interpreted more like a ray starting at linePos, and extending towards lineDir.
Parameters
const float4 &linePosThe source position of the line. const float4 &lineDirThe direction of the line. This vector must be normalized in advance. const float4 &sphereCenterThe center position of the sphere to test. floatsphereRadiusThe radius of the sphere, which must be >= 0. float &t1 [out]This parameter receives the parametric distance along the line to the first point of intersection. If the sphere and the line do not intersect, this variable is not written to. To receive the actual world space point corresponding to this point of intersection, compute the vector 'linePos + t1 * lineDir'.float &t2 [out]This parameter receives the parametric distance along the line to the second point of intersection. If the sphere and the line do not intersect, this variable is not written to. If the line is tangent to this sphere (one point of intersection), this variable will be set equal to t1, so that the line segment [t1, t2] always forms a line segment completely enclosed inside the sphere. To receive the actual world space point corresponding to this point of intersection, compute the vector 'linePos + t2 * lineDir'.
Return Value
The number of intersection points: 0, 1 or 2. In case of 0, the line and sphere do not intersect. In case of 1, the line is tangent to the sphere. If the value of 2 is returned, the line properly intersects the sphere.