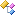 Triangle[Class Summary] |
 a |
| b |
| c |
 ctor (+1 overload) |
| Translate(offset) |
| Transform(transform) (+3 overloads) |
| BarycentricUVW(point)[const] |
| BarycentricUV(point)[const] |
| Point(uvw)[const] (+3 overloads) |
| Centroid()[const] |
| CenterPoint()[const] |
| Area()[const] |
| Perimeter()[const] |
| VertexArrayPtr() (+1 overload) |
| Vertex(i)[const] |
| CornerPoint(i)[const] |
| Edge(i)[const] |
| PlaneCCW()[const] |
| PlaneCW()[const] |
| NormalCCW()[const] |
| NormalCW()[const] |
| UnnormalizedNormalCCW()[const] |
| UnnormalizedNormalCW()[const] |
| AnyPointFast()[const] |
| ExtremePoint(direction)[const] (+1 overload) |
| ToPolygon()[const] |
| ToPolyhedron()[const] |
| BoundingAABB()[const] |
| IsFinite()[const] |
| IsDegenerate(epsilon)[const] |
| Contains(...)[const] (+2 overloads) |
| Distance(point)[const] (+2 overloads) |
| DistanceSq(point)[const] |
| Intersects(...)[const] (+12 overloads) |
| ProjectToAxis(axis,dMin,dMax)[const] |
| UniqueFaceNormals(out)[const] |
| UniqueEdgeDirections(out)[const] |
| ClosestPoint(point)[const] (+3 overloads) |
| ClosestPointToTriangleEdge(...)[const] (+1 overload) |
| RandomPointInside(rng)[const] |
| RandomVertex(rng)[const] |
| RandomPointOnEdge(rng)[const] |
| ToString()[const] |
| SerializeToString()[const] |
| SerializeToCodeString()[const] |
| Equals(rhs,epsilon)[const] |
| BitEquals(other)[const] |
| NumFaces()[static] |
| NumEdges()[static] |
| NumVertices()[static] |
| BarycentricInsideTriangle(uvw)[static] |
| Area2D(p1,p2,p3)[static] |
| SignedArea(point,a,b,c)[static] |
| IsDegenerate(p1,p2,p3,epsilon)[static] |
| IntersectLineTri(...)[static] |
| FromString(str,outEndStr)[static] (+1 overload) |
Triangle::BarycentricUV
Syntax
float2 Triangle::BarycentricUV(const float4 &point) const; [5 lines of code]Expresses the given point in barycentric (u,v) coordinates.
Note
There are two different conventions for representing barycentric coordinates. One uses a (u,v,w) triplet with the equation pt == u*a + v*b + w*c, and the other uses a (u,v) pair with the equation pt == a + u*(b-a) + v*(c-a). These two are equivalent. Use the mappings (u,v) -> (1-u-v, u, v) and (u,v,w)->(v,w) to convert between these two representations.
Parameters
const float4 &pointThe point to express in barycentric coordinates. This point should lie in the plane formed by this triangle.
Return Value
The factors (u,v) that satisfy the weighted sum equation point == a + u*(b-a) + v*(c-a).