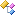 Triangle[Class Summary] |
 a |
| b |
| c |
 ctor (+1 overload) |
| Translate(offset) |
| Transform(transform) (+3 overloads) |
| BarycentricUVW(point)[const] |
| BarycentricUV(point)[const] |
| Point(uvw)[const] (+3 overloads) |
| Centroid()[const] |
| CenterPoint()[const] |
| Area()[const] |
| Perimeter()[const] |
| VertexArrayPtr() (+1 overload) |
| Vertex(i)[const] |
| CornerPoint(i)[const] |
| Edge(i)[const] |
| PlaneCCW()[const] |
| PlaneCW()[const] |
| NormalCCW()[const] |
| NormalCW()[const] |
| UnnormalizedNormalCCW()[const] |
| UnnormalizedNormalCW()[const] |
| AnyPointFast()[const] |
| ExtremePoint(direction)[const] (+1 overload) |
| ToPolygon()[const] |
| ToPolyhedron()[const] |
| BoundingAABB()[const] |
| IsFinite()[const] |
| IsDegenerate(epsilon)[const] |
| Contains(...)[const] (+2 overloads) |
| Distance(point)[const] (+2 overloads) |
| DistanceSq(point)[const] |
| Intersects(...)[const] (+12 overloads) |
| ProjectToAxis(axis,dMin,dMax)[const] |
| UniqueFaceNormals(out)[const] |
| UniqueEdgeDirections(out)[const] |
| ClosestPoint(point)[const] (+3 overloads) |
| ClosestPointToTriangleEdge(...)[const] (+1 overload) |
| RandomPointInside(rng)[const] |
| RandomVertex(rng)[const] |
| RandomPointOnEdge(rng)[const] |
| ToString()[const] |
| SerializeToString()[const] |
| SerializeToCodeString()[const] |
| Equals(rhs,epsilon)[const] |
| BitEquals(other)[const] |
| NumFaces()[static] |
| NumEdges()[static] |
| NumVertices()[static] |
| BarycentricInsideTriangle(uvw)[static] |
| Area2D(p1,p2,p3)[static] |
| SignedArea(point,a,b,c)[static] |
| IsDegenerate(p1,p2,p3,epsilon)[static] |
| IntersectLineTri(...)[static] |
| FromString(str,outEndStr)[static] (+1 overload) |
Triangle::BarycentricUVW
Syntax
float3 Triangle::BarycentricUVW(const float4 &point) const; [55 lines of code]Expresses the given point in barycentric (u,v,w) coordinates.
Note
There are two different conventions for representing barycentric coordinates. One uses a (u,v,w) triplet with the equation pt == u*a + v*b + w*c, and the other uses a (u,v) pair with the equation pt == a + u*(b-a) + v*(c-a). These two are equivalent. Use the mappings (u,v) -> (1-u-v, u, v) and (u,v,w)->(v,w) to convert between these two representations.
Parameters
const float4 &pointThe point of the vector space to express in barycentric coordinates. This point should lie in the plane formed by this triangle.
Return Value
The factors (u,v,w) that satisfy the weighted sum equation point == u*a + v*b + w*c.